GIẢI BÀI TẬP: Đại số
Cho parabol $\left( P \right):y = \frac{-1}{2}{x^2}$ và đường thẳng $(d):y=x-4.$
a) Vẽ $(P)$ và $(d)$ trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của $(P)$ và $(d)$ bằng phép tính.
a) Vẽ $(P)$ và $(d)$ trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của $(P)$ và $(d)$ bằng phép tính.
Hướng dẫn giải
a) Hàm số $y = \frac{1}{2}{x^2}$ có tập xác định $D=R.$
Bảng giá trị

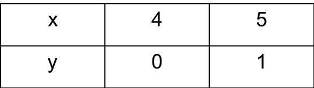
Hàm số $y=x-4$ có tập xác định $D=R.$
Bảng giá trị
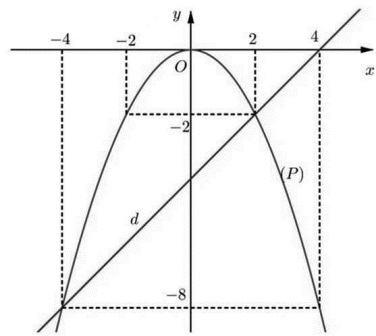
Đồ thị
b) Phương trình hoành độ giao điểm $(P)$ và $(d)$:
$\begin{array}{l}
- \frac{1}{2}{x^2} = x - 4\\
\Leftrightarrow - \frac{1}{2}{x^2} - x + 4\\
\Leftrightarrow \left[ \begin{array}{l}
x = 2 \Rightarrow y = - 2\\
x = - 4 \Rightarrow y = - 8
\end{array} \right.
\end{array}$
Vậy $(P)$ cắt $(d)$ tại hai điểm có tọa độ lần lượt là $(2;-2)$ và $(-4;-8).$
Bảng giá trị

Hàm số $y=x-4$ có tập xác định $D=R.$
Bảng giá trị

Đồ thị

b) Phương trình hoành độ giao điểm $(P)$ và $(d)$:
$\begin{array}{l}
- \frac{1}{2}{x^2} = x - 4\\
\Leftrightarrow - \frac{1}{2}{x^2} - x + 4\\
\Leftrightarrow \left[ \begin{array}{l}
x = 2 \Rightarrow y = - 2\\
x = - 4 \Rightarrow y = - 8
\end{array} \right.
\end{array}$
Vậy $(P)$ cắt $(d)$ tại hai điểm có tọa độ lần lượt là $(2;-2)$ và $(-4;-8).$



