I. Các đại lượng về góc xác định chuyển động quay
1. Tọa độ góc
Trong chuyển động quay của vật rắn quanh trục cố định:
- Các điểm trên trục quay luôn nằm yên.
- Các điểm khác vạch các đường tròn có trục là trục quay và quay các góc bằng nhau trong cùng khoảng thời gian. 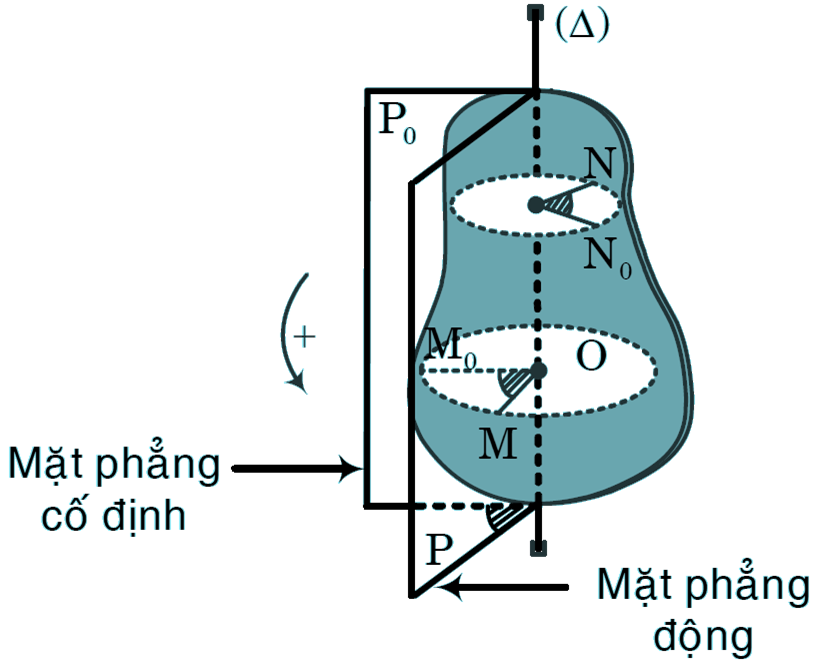
Ở mỗi thời điểm, vị trí của vật rắn được xác định bởi tọa độ góc $\varphi $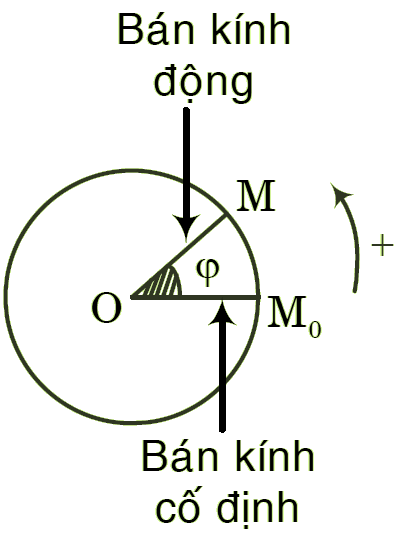
 2. Tốc độ góc
2. Tốc độ góc
- Tốc độ góc trung bình
${\omega _{tb}} = \frac{{{\Delta _\varphi }}}{{{\Delta _t}}}$
- Tốc độ góc tức thời
$\omega = \mathop {\lim }\limits_{{\Delta _t} \to 0} \frac{{{\Delta _\varphi }}}{{{\Delta _t}}} = \frac{{{d_\varphi }}}{{{d_t}}} = \varphi '$
(Đơn vị: rad/s hoặc $rad.{s^{ - 1}}$)
3. Gia tốc góc
- Gia tốc góc trung bình
${\gamma _{tb}} = \frac{{{\Delta _\omega }}}{{{\Delta _t}}}$
- Gia tốc góc tức thời
$\gamma = \mathop {\lim }\limits_{{\Delta _t} \to 0} \frac{{{\Delta _\omega }}}{{{\Delta _t}}} = \frac{{{d_\omega }}}{{{d_t}}} = \omega ' = \varphi '$
(Đơn vị: rad/$s^2$ hoặc $rad.{s^{ - 2}}$)
II. Các phương trình động học của chuyển động quay
1. Chuyển động quay đều
$\gamma = 0$
$\omega = $ không đổi
$\varphi = \omega t + {\varphi _o}$
2. Chuyển động biến đổi đều
$\gamma = $ không đổi
$\omega = \gamma t + {\omega _o}$
$\varphi = \frac{1}{2}\gamma {t^2} + {\omega _o}t + {\varphi _o}$
${\omega ^2} - {\omega _o}^2 = 2\gamma \left( {\varphi - {\varphi _o}} \right)$
${\omega _o},{\varphi _o}:$ tốc độ góc ban đầu; tọa độ góc ban đầu
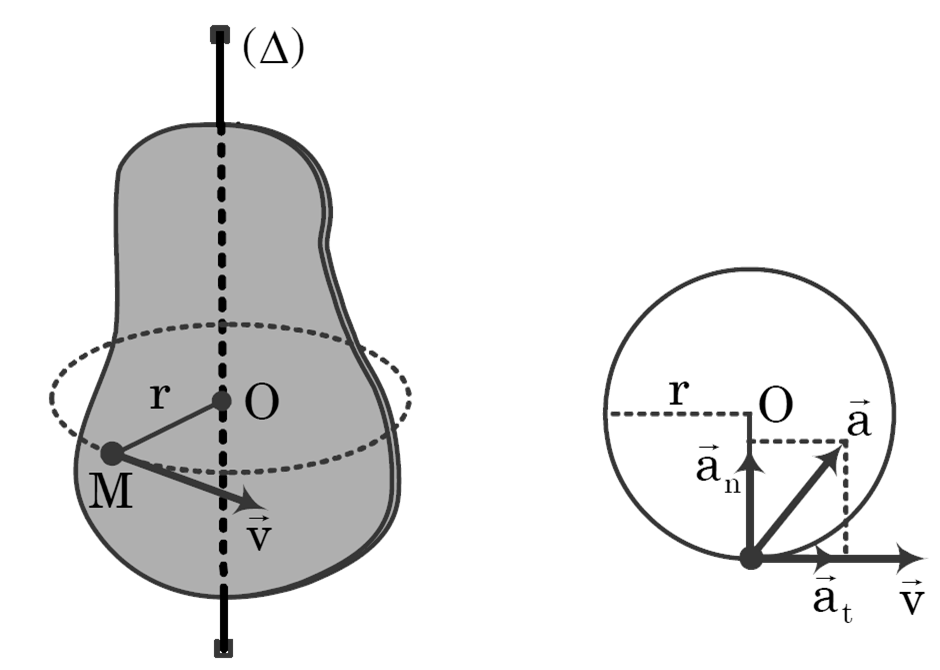
III. Vận tốc và gia tốc của một điểm
Ví dụ: Một vật rắn quay chậm dần đều quanh trục cố định. Tốc độ góc biến thiên từ 780 vòng/ phút trở thành 60 vòng/ phút trong 2 phút.
a. Tính gia tốc của chuyển động
b. Tính số vòng quay trong 2 phút đó và số vòng quay đến lúc dừng lại.
Hướng dẫn
a. Gia tốc góc:
Ta có:
${\omega _1} = \frac{{780.2\pi }}{{60}} = 26\pi \left( {rad/s} \right)$
${\omega _2} = \frac{{60.2\pi }}{{60}} = 2\pi \left( {rad/s} \right)$
$ \Rightarrow \gamma = \frac{{{\omega _1} - {\omega _2}}}{{{\Delta _t}}} = \frac{{ - 24\pi }}{{2.60}} = - \frac{\pi }{5}\left( {rad/{s^2}} \right)$
b. Số vòng quay:
Áp dụng công thức ${\omega _2}^2 - {\omega _1}^2 = 2\gamma \Delta \varphi $
* Trong 2 phút:
$\begin{gathered}
\Delta \varphi = \frac{{{{\left( {2\pi } \right)}^2} - {{\left( {26\pi } \right)}^2}}}{{2\left( { - \frac{\pi }{5}} \right)}} = 1680\pi \,rad \hfill \\
= \frac{{1680\pi }}{{2\pi }} = 840\,\left({vòng} \right) \hfill \\
\end{gathered} $
* Đến lúc dừng:
$\begin{gathered}
\Delta \varphi ' = \frac{{ - {{\left( {26\pi } \right)}^2}}}{{2\left( { - \frac{\pi }{5}} \right)}} = 1690\pi \,rad \hfill \\
= \frac{{1690\pi }}{{2\pi }} = 845\,\left( {vòng} \right) \hfill \\
\end{gathered} $



